6 x 10 = 60
6 x 100 = 600
6 x 1,000 = 6,000
6 x 10,000 = 60,000
My students themselves have said that you "add a zero" each time. We have talked about the fact that adding a zero means 60 + 0, which is not 600, and they have made representations of these kinds of problems as arrays in order to see the increasing magnitude (ten times bigger) as one of the factors is multiplied by 10.
After these conversations and explorations, I've been looking to see what my students do when multiplying 4 digit numbers by 1 digit numbers. Last week, when I took their work home to look at, I found this (as one step of a longer problem):
Many Tweeps wondered what this student, who I'll call Shayla, was thinking about, so the next day I asked her. I took notes, then promptly lost my notes, then asked her to repeat her explanation. Each time I beckoned her over she rolled her eyes, but she smiled too. She liked knowing a bunch of teachers were wondering about her thinking.
"Well," she said, "2 x 7 is 14, and 14 x 10 is 140, which is the same as 20 x 7. And 140 x 10 is 1,400, which is the same as 200 x 7. And 1,400 x 10 is 14,000, which is the same as 2,000 x 7, which is what I figuring out."
"How did you decide how many times to multiply by 10?" I asked.
"Umm, because there were three..." she trailed off, her finger waving above the zeros in 2,000. "I don't know what to call these. The two was three..."
"Sometimes we call them 'places,'" I suggested. "You know how we say this is the ones place, and this is the tens place, and this is the hundreds place. Does that sound right?"
"Yes," she said. "There were three places here before the 2. So I multiplied by 10 one time for each place."
"And why did you put three checks there?" I asked, because some of us had wondered if she put them there to keep track of the "places."
"Because Aliyah and I got different answers, so we were checking it over and over again to figure out where we made a mistake," she explained in a tone that said this is so obvious.
Here is the whole of her work on that problem:
[Here is the slideshow about refugees arriving in Europe via the Mediterranean Sea, which connects to our social studies unit on immigration.]
Here's what's interesting to me about this: once again, I thought that if students saw this pattern one or two times, they would internalize it and trust it, and not need to go through all those steps of repeatedly multiplying by 10. Some of my students don't need to go through these steps, but there are maybe 5 or 6 who are doing this each time they have to multiply a 4-digit number. Here are a few examples:
They don't trust the pattern yet. This is just like first graders who need to count groups of 10 by ones over and over again until they finally trust that a group of 10 is always a group of 10. They need to go through that process enough times, and they need to be given that time.
The other night, when I found myself solving problems in base 2 through the Exploding Dots project, I found that I didn't trust the pattern either. I needed to walk through each step for each problem. If someone had told me I had to skip the steps I wanted to go through and following a quicker procedure, I could have followed the procedure, but I wouldn't have understood it deeply.
The next day, by the way, here's what Shayla did:
She's starting to be able to skip a few steps. Trusting the pattern. But in 8 days, I won't be her teacher anymore, and I shudder to think how quickly another teacher will tell her, as she faces bigger factors, that she can just "add zeros" for each place.





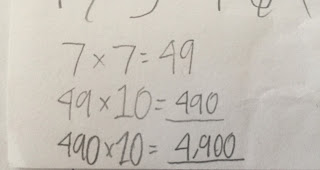

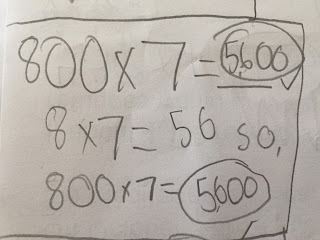
I have not told them that you "add a zero" in order to multiply by a multiple of 10 (I wouldn't dream of it!), but I would not be surprised if other people have told them that.
ReplyDeleteThe more I think about this, the more slippery the issue with saying "add a zero" has become to me. What exactly is wrong with it? So it's a rule that expires? Every rule expires, and this one is even particularly sturdy -- it's true for whole numbers. Anyway I don't want to get side-railed but I think we can be good, student-centered teachers that say "add a zero."
Back to your post...
It's interesting. I'm trying to think about what it means to "trust a pattern." Part of what that means to me is that you already SEE and NOTICE the pattern, but you're not sure if you believe it yet. And I'm wondering if we think that's true of your kids? Or are they just not yet seeing the "summary" pattern, that would allow them to skip the steps?
This reminds me of Anna Sfard's idea that a lot of math learning is turning processes into object. At first, we have routines, procedures, little algorithms that we use to think about math. And then we start noticing these procedures AS procedures, things that we can look at, summarize, and describe. And then those procedures become objects of study for us, and we can skip through them. With our help, kids can learn to summarize and treat this entire "multiply by 10 for each place" as just one THING that they can skip through.
By the way, I love that you gave your student the language of "place" as a more mathematically sophisticated bit of language, in place of "zero." That's smart and I don't know if I've realized that you can do that before.
Thanks for an awesome post! (Also, some of the pics aren't appearing on my screen.)
Thanks for your comment, Michael. I have to admit I figure problems like that out by counting the zeros and "adding" them on when I multiply. I do know what it means when I do it, although I don't think about what it means each time.
DeleteI'd rather that they learn the reasons why they follow that rule at the same time that they discover the pattern and learn to trust it. It's okay with me if they use that rule of counting the zeros and "adding" them, but I definitely want them to be able to explain why we do that.
Some of my students know that, for example, 6 x 10 = 60, but they aren't sure if 50 x 10 = 500. They have to figure out what 50 x 10 is. Is that because they don't see the pattern or don't trust it? I'm not sure. I think it has to do with fewer experiences of multiplying larger numbers (or even counting them, I suspect). When I taught second grade we would practice adding and subtracting 10 from a number all the time. And what would happen would be that a student would see the pattern and would start to be able to quickly add 10 to a number on Monday, say. But then on Tuesday when I asked again, they would have to think about it or count on their fingers or use the hundreds chart. It took days and days, sometimes weeks or months, of doing this over and over again before some of them would automatically know the sum when you add 10 to a number. It always used to surprise me, no matter how many times it happened, because it seems so obvious to me. But when I was working in base 2 the other night I was reminded of that feeling -- wait, I think I see the pattern, but I don't really BELIEVE yet that it is the right answer unless I go through the steps myself.
Glad you like the language of "place." I had a moment when I wondered what the heck to call it, and then that came to me, and it made sense to her.
Thanks for telling me about the pictures! I think they are working now. Somehow they seemed to work yesterday but not today, so I reuploaded them.
Thanks for reading.
This comment has been removed by the author.
ReplyDelete