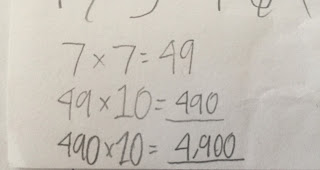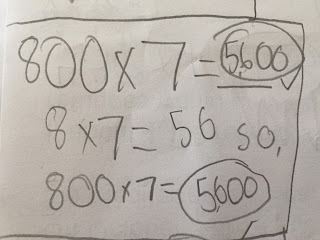6 x 10 = 60
6 x 100 = 600
6 x 1,000 = 6,000
6 x 10,000 = 60,000
My students themselves have said that you "add a zero" each time. We have talked about the fact that adding a zero means 60 + 0, which is not 600, and they have made representations of these kinds of problems as arrays in order to see the increasing magnitude (ten times bigger) as one of the factors is multiplied by 10.
After these conversations and explorations, I've been looking to see what my students do when multiplying 4 digit numbers by 1 digit numbers. Last week, when I took their work home to look at, I found this (as one step of a longer problem):
Many Tweeps wondered what this student, who I'll call Shayla, was thinking about, so the next day I asked her. I took notes, then promptly lost my notes, then asked her to repeat her explanation. Each time I beckoned her over she rolled her eyes, but she smiled too. She liked knowing a bunch of teachers were wondering about her thinking.
"Well," she said, "2 x 7 is 14, and 14 x 10 is 140, which is the same as 20 x 7. And 140 x 10 is 1,400, which is the same as 200 x 7. And 1,400 x 10 is 14,000, which is the same as 2,000 x 7, which is what I figuring out."
"How did you decide how many times to multiply by 10?" I asked.
"Umm, because there were three..." she trailed off, her finger waving above the zeros in 2,000. "I don't know what to call these. The two was three..."
"Sometimes we call them 'places,'" I suggested. "You know how we say this is the ones place, and this is the tens place, and this is the hundreds place. Does that sound right?"
"Yes," she said. "There were three places here before the 2. So I multiplied by 10 one time for each place."
"And why did you put three checks there?" I asked, because some of us had wondered if she put them there to keep track of the "places."
"Because Aliyah and I got different answers, so we were checking it over and over again to figure out where we made a mistake," she explained in a tone that said this is so obvious.
Here is the whole of her work on that problem:
[Here is the slideshow about refugees arriving in Europe via the Mediterranean Sea, which connects to our social studies unit on immigration.]
Here's what's interesting to me about this: once again, I thought that if students saw this pattern one or two times, they would internalize it and trust it, and not need to go through all those steps of repeatedly multiplying by 10. Some of my students don't need to go through these steps, but there are maybe 5 or 6 who are doing this each time they have to multiply a 4-digit number. Here are a few examples:
They don't trust the pattern yet. This is just like first graders who need to count groups of 10 by ones over and over again until they finally trust that a group of 10 is always a group of 10. They need to go through that process enough times, and they need to be given that time.
The other night, when I found myself solving problems in base 2 through the Exploding Dots project, I found that I didn't trust the pattern either. I needed to walk through each step for each problem. If someone had told me I had to skip the steps I wanted to go through and following a quicker procedure, I could have followed the procedure, but I wouldn't have understood it deeply.
The next day, by the way, here's what Shayla did:
She's starting to be able to skip a few steps. Trusting the pattern. But in 8 days, I won't be her teacher anymore, and I shudder to think how quickly another teacher will tell her, as she faces bigger factors, that she can just "add zeros" for each place.